Medición sin contacto de la temperatura en superficies metálicas mediante infrarrojos
Cumplir determinadas temperaturas es un factor que define el proceso y la calidad en casi todas las fases de la producción industrial. Los termómetros infrarrojos de medición sin contacto son muy conocidos para medir la temperatura. Esto también se aplica a la medición de metales. Un seguimiento y control adecuados de las temperaturas de proceso requiere una muy buena orientación por parte del fabricante o conocimientos básicos sobre las técnicas de medición por parte del cliente. En el siguiente artículo se explicarán parámetros importantes, como la emisividad y la reflexión, así como las causas de los errores de medición. También se mostrará la influencia en la medición de metales y se expondrá por qué es posible una medición fiable y reproducible.
Después del tiempo, la temperatura es la propiedad física que se mide con más frecuencia. Los dispositivos de medición de temperatura por infrarrojos definen las temperaturas a través de la radiación infrarroja emitida por el objeto, sin entrar en contacto con él. Pero, ¿cómo funciona la medición de temperatura sin contacto? ¿Cuáles son los retos de la medición de superficies metálicas?
El conjunto de radiación infrarroja
Cada cuerpo con una temperatura superior al cero absoluto de 0 K (-273,15°C) emite una radiación electromagnética desde su superficie que es proporcional a su temperatura intrínseca. El conjunto de radiaciones infrarrojas sólo cubre una parte limitada dentro del conjunto total de radiaciones electromagnéticas. Comienza en el rango visible de unos 0,78 μm y termina en longitudes de onda de aproximadamente 1000 μm. Las longitudes de onda comprendidas entre 0,7 y 14 μm son importantes para medir la temperatura por infrarrojos. Por encima de estas longitudes de onda, el nivel de energía es tan bajo que los detectores no son lo suficientemente sensibles para detectarlas, como puede verse en la ilustración.
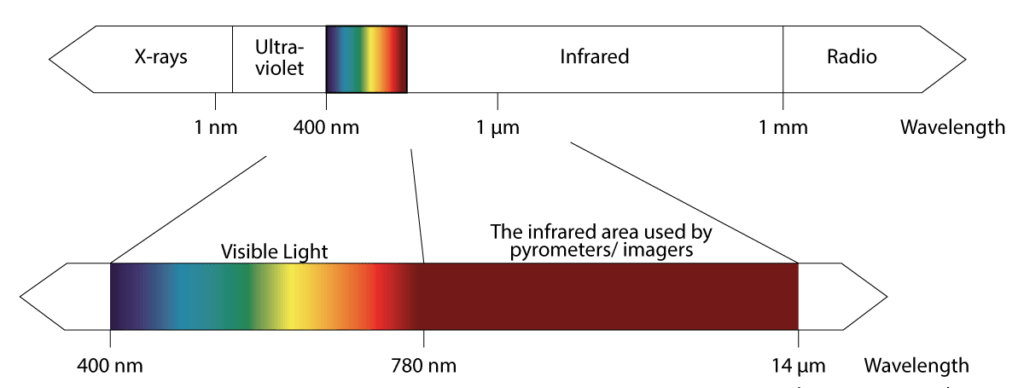
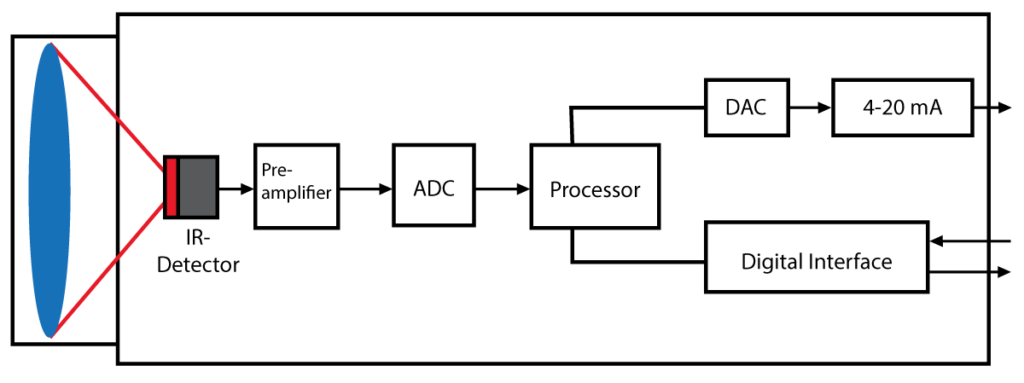
La radiación del cuerpo penetra en la atmósfera y puede enfocarse en un elemento detector con ayuda de una lente. El elemento detector genera una señal eléctrica proporcional a la radiación. Esta señal se amplifica y, mediante un tratamiento digital sucesivo de la señal digital, se transforma en una señal de salida proporcional a la temperatura del objeto. El valor medido puede mostrarse en una pantalla o emitirse como señal.
Las salidas normalizadas para transmitir los resultados de las mediciones a los sistemas de control están disponibles en forma de señal lineal 0/4-20 mA, 0-10 V y como señal de termopar. Además, la mayoría de los termómetros de infrarrojos utilizados actualmente ofrecen interfaces digitales (USB, RS232, RS485) para el posterior procesamiento digital de la señal y para poder acceder a los parámetros del dispositivo.
El comportamiento de la radiación infrarroja sobre las superficies metálicas se examina con más detalle en los párrafos siguientes. Previamente, se presentará el detector y la conversión de la señal en temperatura del objeto.
Cálculo de la temperatura mediante radiación infrarroja
El detector como captador de radiación identifica el elemento más importante de cada termómetro de infrarrojos. Una señal se origina a través de una radiación electromagnética que aparece y que es completamente evaluable. La señal del detector U se conecta con la temperatura del objeto TObject de la siguiente manera:![]()
La señal del detector que resulta de la radiación emitida por un objeto dentro del conjunto de radiación total, aumenta proporcionalmente a la cuarta potencia de la temperatura absoluta del objeto. Es decir: Si la temperatura del objeto de medición se duplica, la señal del detector se multiplicará por 16.
La fórmula cambia, ya que también hay que tener en cuenta la emisividad ε del objeto y la radiación ambiente reflectante de la superficie del objeto TAmbient, así como la radiación propia del termómetro de infrarrojos TPyro:![]()
Además, los termómetros de infrarrojos no funcionan en todo el campo de radiación. El exponente depende de la longitud de onda. N representa la longitud de onda de 1 a 14 μm en el rango de 17…2, para los dispositivos de medición de onda corta para la definición de la temperatura del metal (1,0 a 2,3 μm) el rango está entre 15…17:![]()
La temperatura del objeto surge debido a un desplazamiento de la última fórmula mencionada. Los resultados de estos cálculos se guardan como una matriz de curvas en la EEPROM del termómetro de infrarrojos para todas las temperaturas que se producen:
![]()
Por lo tanto, los termómetros de infrarrojos reciben suficiente señal para medir la temperatura. De la fórmula se desprende que, además de la gama de longitudes de onda (matriz de radiación), la radiación ambiental reflectante y la emisividad son fundamentales para una medición precisa de la temperatura. La importancia de estos parámetros se deducirá y explicará a continuación.
El cuerpo negro como referencia de importancia
Ya hacia 1900, Planck, Stefan, Boltzmann, Wien y Kirchhoff definieron con más detalle el espectro electromagnético y establecieron coherencias cualitativas y cuantitativas para la descripción de la energía infrarroja. El cuerpo negro constituye la base para la comprensión de los fundamentos físicos de la tecnología de medición de temperatura sin contacto y para la calibración de termómetros infrarrojos.
Por un lado, el cuerpo negro es un cuerpo que absorbe toda la radiación que se produce. Ni la reflexión (ρ = 0) ni la transmisión (τ = 0) aparecen en el cuerpo. Por otra parte, el cuerpo negro emite un máximo de la energía posible para cada longitud de onda, en función de su propia temperatura. La construcción de un cuerpo negro es sencilla. Un cuerpo hueco térmico tiene un pequeño orificio en un extremo. Si el cuerpo se calienta y alcanza una determinada temperatura, en el interior de la cámara hueca se propaga una temperatura equilibrada.
La ley de radiación de Planck muestra la correlación básica para las mediciones de temperatura sin contacto: Describe la radiación espectral específica Mλs del cuerpo negro en el semiespacio en función de su temperatura T y de la longitud de onda λ (c: velocidad de la luz, h: constante de Plank):
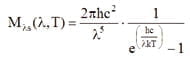
La segunda coherencia, que se desprende del esquema gráfico, es que la longitud de onda que constituye el máximo de radiación se desplaza hacia la zona de onda corta cuando aumentan las temperaturas. Este comportamiento subyace a la ley de desplazamiento de Wien y puede derivarse de la ecuación de Plank mediante diferenciación.La alta radiación es, por tanto, una razón -aunque no la más vital- por la que las superficies metálicas pueden medirse con longitudes de onda cortas a altas temperaturas. El largo intervalo de fluctuación también es de alta intensidad. La emisividad, la reflexión y su influencia en los errores de medición tienen un impacto mucho mayor, ya que los metales son emisores selectivos. La alta radiación es, por tanto, una razón -aunque no la más vital- por la que las superficies metálicas pueden medirse con longitudes de onda cortas a altas temperaturas. El largo intervalo de fluctuación también es de alta intensidad. La emisividad, la reflexión y su influencia en los errores de medición tienen un impacto mucho mayor, ya que los metales son emisores selectivos.

Superficies metálicas como emisores selectivos
En realidad, sólo unos pocos cuerpos cumplen el ideal del cuerpo negro. En la práctica, para la calibración del sensor se utilizan superficies de radiación que alcanzan emisividades de hasta 0,99 dentro de la zona de longitud de onda solicitada. La temperatura del objeto puede definirse a través de la medida de radiación de la emisividad ε (Epsilon) que establece la relación del valor real de radiación del objeto y el del cuerpo negro para la misma temperatura. De este modo, la emisividad está siempre entre cero y uno; la parte de radiación que falta se compensa mediante la indicación de la emisividad.
Muchas de las superficies que se van a medir tienen una emisividad constante en todas las longitudes de onda, pero emiten menos radiación en comparación con el cuerpo negro. Se denominan cuerpo gris. Varios sólidos no metálicos presentan una emisividad elevada y relativamente constante en el rango espectral de onda larga, independientemente de su estado superficial.
Los objetos , por ejemplo superficies metálicas, cuya emisividad depende entre otras cosas de la temperatura y la longitud de onda se denominan emisores selectivos. Hay una serie de razones importantes por las que la medición en metales sólo debe realizarse en la gama de ondas cortas. En primer lugar, las superficies metálicas a altas temperaturas, así como de longitud de onda corta (2,3 μm; 1,6 μm; 1,0 μm) no sólo consisten en la mayor radiación, sino también en la mayor emisividad. En segundo lugar, se ajustan a la emisividad de los óxidos metálicos para que las diferencias de temperatura, evocadas por el cambio de emisividad (tinte térmico), se reduzcan al mínimo.

Otra influencia importante en la decisión de un termómetro infrarrojo de onda corta es que los metales, en comparación con otros materiales, pueden presentar emisividades desconocidas. Los dispositivos de onda corta reducen considerablemente los errores de medición en las emisividades mal ajustadas.
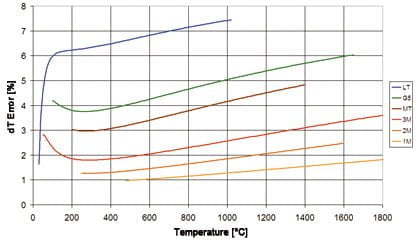
Mediciones reproducibles a pesar de la reflexión
Cuanto menor sea la emisividad de una superficie, mayor será la radiación reflejada que reciba el termómetro de infrarrojos del entorno. Como la mayoría de los cuerpos, como los metales, no tienen una transmisión dentro de la gama infrarroja, se aplica la fórmula siguiente:
ε + p = 1
En este caso, ε es la emisividad y ρ la reflexión. La radiación infrarroja, que es evaluada por el aparato y convertida en temperaturas, no sólo está influenciada por la emisividad de la superficie metálica (y la cuota de radiación compensada), sino que también es crucial a través de objetos calientes del entorno (TAmbient), como componentes y hornos.
El parámetro TAmbient debe considerarse con más cuidado cuanto menor sea la temperatura de la superficie metálica que se va a medir y cuanto mayor sea la temperatura reflejada del entorno. La cantidad de reflexión está de facto normalmente dirigida y, por tanto, es fácil de determinar.
La cantidad de reflexión puede establecerse como un tamaño y garantiza resultados de medición reproducibles.
Los termómetros de infrarrojos en la práctica: Endurecimiento inductivo y procesos de inducción
Un ejemplo para la medición de superficies metálicas es el tratamiento térmico sobre el endurecimiento por inducción. Durante este proceso, un componente se coloca en un fuerte campo alterno y allí se calienta y se congela en la estructura solicitada. Es posible ajustar la penetración del calor en el material localmente mediante el control de la frecuencia; sólo se tratan partes del componente. La estructura solicitada del metal depende de un proceso ideal de temperatura-tiempo, por lo que es vital controlar permanentemente la temperatura.
Los parámetros importantes de un termómetro de infrarrojos son:
- El cabezal sensor está separado de la caja electrónica, por lo que el campo electromagnético no influye en los resultados de la medición.
- Longitud de onda (1,0 μm / 1,6 μm / 2,3 μm) especialmente para superficies metálicas.
- Compensación de la temperatura ambiente (TAmbient), por ejemplo, mediante la temperatura de referencia
- Medición fiable de la temperatura de metales desde 50°C hasta 1800°C
- Control rápido de la temperatura mediante mediciones en 1 ms
- Medición de componentes pequeños mediante alta resolución óptica (tamaños de medición a partir de 0,7 mm) y marcado de tamaño de punto mediante doble puntería láser

Termómetros infrarrojos Optris para medir la temperatura del metal
Optris ofrece una amplia gama de pirómetros para metales, así como cámaras de infrarrojos para numerosas aplicaciones en la industria metalúrgica.

Medición de alta temperatura en metal
Los siguientes termómetros de infrarrojos son perfectamente adecuados para la medición de temperaturas muy elevadas en metales, óxidos metálicos y cerámica:
- Pirómetro optris CT 1M / 2M: 250°C … 2.200°C*.
- Pirómetro optris CTlaser 1M / 2M con innovador láser doble: 250 °C … 2.200 °C*.
- Termómetro de mano optris P20 1M / 2M: 385 °C … 1.800 °C*.
- Pirómetro de relación optris CTratio 1M: 700 °C … 1.800 °C
Mediciones a baja temperatura en metal
Varias aplicaciones de la industria metalúrgica tienen lugar a temperaturas más bajas. Para estas necesidades, Optris ofrece los siguientes termómetros infrarrojos:
- Pirómetro optris CT 3M: 50 °C … 1.800 °C
- Pirómetro optris CTlaser 3M con innovador láser doble: 50 °C … 1.800 °C*.
Medición de metales fundidos
Gracias a sus longitudes de onda de medición extremadamente cortas, los siguientes pirómetros son perfectos para medir la temperatura de metales fundidos:
- Pirómetro optris CTlaser 05M: 1.000 °C … 2.000 °C
- Termómetro de mano optris P20 05M: 1.000 °C … 2.000 °C
Cámaras térmicas para mediciones en metal
Las cámaras termográficas de la serie optris PI ofrecen dispositivos especiales también para mediciones de temperatura en metal, que cubren los siguientes rangos de temperatura:
- Cámara de infrarrojos Optris PI 1M: 450 °C … 1800 °C*.
- Cámara de infrarrojos Optris PI 05M: 900 °C … 2000 °C*.